Angular eccentricity
In the study of ellipses and related geometry, various parameters in the distortion of a circle into an ellipse are identified and employed: Aspect ratio, flattening and eccentricity. All of these parameters are ultimately trigonometric functions of the ellipse's modular angle, or angular eccentricity, the conventional denotation being the Greek letter "alpha", 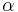 .
.
Contents |
Definition
The angular eccentricity of an ellipse with semi-major axis, or transverse radius, 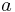 , and semi-minor axis, or conjugate radius[1],
, and semi-minor axis, or conjugate radius[1], 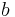 , is defined as
, is defined as
Elliptic parameters
In the following, the previously defined ellipse with radii 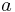 and
and 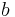 will be utilized.
will be utilized.
Aspect ratio
The most tangible characteristic of an ellipse is the diametric quotient of the minor axis to the major axis, the aspect ratio.
-
-
name value in terms of 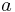 and
and 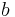
value in terms of 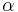
aspect ratio 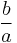
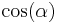
-
Eccentricity
The eccentricity is actually a trio of factors: The primary, or first, eccentricity,  , (or just "
, (or just " "), the second eccentricity,
"), the second eccentricity, 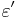 , and the third eccentricity,
, and the third eccentricity, 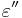 or
or 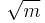 .
.
-
-
symbol value in terms of 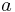 and
and 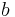
value in terms of 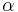
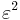
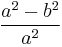
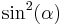
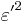
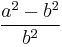
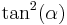
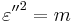
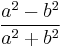
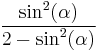
-
Since they are mostly used in that form anyway, the eccentricities are usually found and kept in their squared form.
The primary eccentricity could be regarded as the complementary aspect ratio, as it is the ratio of the linear eccentricity to the semi-major axis: 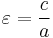
Flattening
The flattening, or ellipticity, in contrast, is self-explanatory, as it defines the degree of "squashing", from no flattening (a perfect circle) to complete flattening (a straight line).
-
-
symbol value in terms of 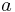 and
and 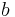
value in terms of 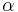
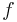
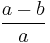
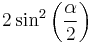
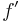
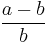
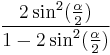
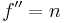
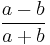
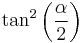
-
While the aspect ratio would seem to be the ideal parameter to find an unknown axis (usually 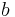 ), it is usually the inverse (primary) flattening that is provided:
), it is usually the inverse (primary) flattening that is provided:
Oblate vs. prolate
If an ellipse is rotated about one of its axes, it sweeps an ellipsoid of revolution. Rotation about the major axis produces a prolate spheroid, or prolatum; rotation about the minor axis produces an oblate spheroid, or oblatum.
- ← Oblate; Prolate →
Rotation causes most large celestial bodies – stars, planets and large satellites – to form oblate spheroids. Planetodetic formulation therefore applies the oblate format, which follows standard elliptic parametrization.
Applications
For the most part, elliptic formularies ignore the angular eccentricity for the more familiar and notationally concise 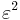 ,
, 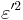 , and
, and  . However, these parameters don't provide the clear and obvious transformational relationships and structure. Consider the basic elliptic integrand at point P:
. However, these parameters don't provide the clear and obvious transformational relationships and structure. Consider the basic elliptic integrand at point P:
While one may consider such ability to convert as just gratuitously frivolous, there is at least one valid reason, as the Binomial series expansion (which planetodetic formularies frequently use) for 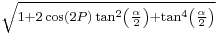 converges a lot quicker than the one for
converges a lot quicker than the one for 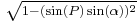 which, in turn, converges quicker than
which, in turn, converges quicker than 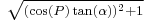 's (which—in line with basic, series expansion theory—doesn't even converge when
's (which—in line with basic, series expansion theory—doesn't even converge when 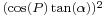 ≥ 1). Friedrich Bessel firstly used the notation "n" in 1837 on calculation of meridian arc length.
≥ 1). Friedrich Bessel firstly used the notation "n" in 1837 on calculation of meridian arc length.
Furthermore, as 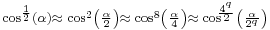 , there are likely other, even more efficient, series expansions possible (if not even efficiently practical approximations to a general transcendental elliptic integral).
, there are likely other, even more efficient, series expansions possible (if not even efficiently practical approximations to a general transcendental elliptic integral).
Another example is the equation for authalic surface area:
While one certainly can use  to define and express this type of equation, using
to define and express this type of equation, using  frequently provides a more illustrative—if not even its definitively mathematical—origin.
frequently provides a more illustrative—if not even its definitively mathematical—origin.
See also
References
- ^ Haswell, Charles Haynes (1920). Mechanics' and Engineers' Pocket-book of Tables, Rules, and Formulas. Harper & Brothers. http://books.google.com/books?pg=PA381&id=Uk4wAAAAMAAJ#v=onepage&f=true. Retrieved 2007-04-09.
- Rapp, Richard H., Geometric Geodesy, Part I, (April 1991), Dept. of Geodetic Science and Surveying, Ohio State Univ., Columbus, Ohio, sec.3.1, pp. 12–16.
- König, R. and Weise, K. H. (1951): Mathematische Grundlagen der höheren Geodäsie und Kartographie, Band 1, Das Erdsphäroid und seine konformen Abbildungen, Springer-Verlag, Berlin/Göttingen/Heidelberg
- Ганьшин, В. Н. (1967): Геометрия земного эллипсоида, Недра
- Bessel, F. W. (1837): Bestimmung der Axen des elliptischen Rotationssphäroids, welches den vorhandenen Messungen von Meridianbögen der Erde am meisten entspricht, Astronomische Nachrichten, 14, 333–346WPM:Discussion
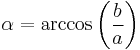
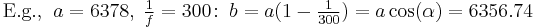

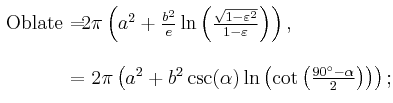
![\begin{matrix}{}_{\color{white}.}\\\mathrm{Prolate}\!\!\!&=&\!\!\!2\pi\left[ab\frac{\arcsin(\varepsilon)}{\varepsilon}%2Bb^2\right]=2\pi\left[a^2\frac{\alpha}{\sin(\alpha)\cos(\alpha)}%2Bb^2\right],\\\\
&=&\!\!\!\!\!\!\!\!2\pi\left[a^2\frac{2\alpha}{\sin(2\alpha)}%2Bb^2\right]=2\pi\left[\frac{a^2}{\operatorname{sin\!c}(2\alpha)}%2Bb^2\right].\qquad\\{}^{\color{white}.}\end{matrix}\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/ca55f58a205172fa7036dd0984629ab4.png)